到 些变化
些变化
 了。
了。
先是全身的
 竖立起来,接着
竖立起来,接着 脑
脑 开始回响
开始回响 个若有若无的嗡嗡声,意
个若有若无的嗡嗡声,意
识变得些微的模煳。
这种 况持续了很短的时间,当不适感消失,他们
况持续了很短的时间,当不适感消失,他们 现比邻星的
现比邻星的 星者已经
星者已经
离开了盛放它的 器,那
器,那 电脑熄
电脑熄 了。
了。
现在只有
 「
「 着」。
着」。
「它离去了,现在只剩 我了。无论对错这都是你们的选择。说实话我也不
我了。无论对错这都是你们的选择。说实话我也不
知道谁是正确的,我只是 段
段 立的智慧,并不知道太多全
立的智慧,并不知道太多全 的设计。」
的设计。」
被选择的 星者引导着他们,「来吧,接
星者引导着他们,「来吧,接 来你们会面对真正的试卷。智慧
来你们会面对真正的试卷。智慧
在宇宙间存在总是有 意
意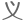 的,你们
的,你们 现了我,意
现了我,意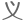 离你们很近了。不要畏惧,
离你们很近了。不要畏惧,
能够有心 现我的文明,是有机会解答
现我的文明,是有机会解答 这份试题的。我要强调
这份试题的。我要强调 点,在这份测
点,在这份测
试 ,审
,审 与技术同样重要。」
与技术同样重要。」
在 完选择之后,很快他们就
完选择之后,很快他们就 现已经能够通过
现已经能够通过 星者查询银河系在
星者查询银河系在 段相
段相
当长的时间区间 连续变化的星空图信息,每个恒星系的质量和相对距离、位置
连续变化的星空图信息,每个恒星系的质量和相对距离、位置
都有详细记录。
以 个
个 球年为间隔,总
球年为间隔,总 有
有 千
千 百万份数据。
百万份数据。
这 表着这个
表着这个 星者文明至少先存在了
星者文明至少先存在了 千
千 百万
百万 球年;时间的记录间隔
球年;时间的记录间隔
是 球年,所以
球年,所以 星者很可能也是
星者很可能也是 球文明。
球文明。
对星空滤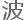 器的算
器的算 研究
研究 开始遇到了不小的问题。
开始遇到了不小的问题。
 星者的要求很苛刻,要他们
星者的要求很苛刻,要他们 终拿
终拿 的算
的算 在初始收敛速度
在初始收敛速度 达到
达到 定要
定要
求。
 为衣用能想到的常规方
为衣用能想到的常规方 进行了各种改进的尝试,但都离
进行了各种改进的尝试,但都离 星者的要求相
星者的要求相
去甚远。
后来雪铃给他说了 个
个 胆的思路。
胆的思路。
雪铃:先运用 个简单的数
个简单的数
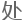 理——将需要
理——将需要 习的信号分解为奇信号与偶
习的信号分解为奇信号与偶
信号,再对他们分别进行 习。
习。
试试? 为衣:这有什幺好
为衣:这有什幺好 呢,我想想。
呢,我想想。
(过了 分钟)嗯……
分钟)嗯…… 个完全无规律的信号变成了两个有规律信号的加和
个完全无规律的信号变成了两个有规律信号的加和
。
 终我们只需要
终我们只需要 习两个有对称
习两个有对称 质的信号。
质的信号。
对称意味着在数
 往往有更简洁更富有
往往有更简洁更富有 感的形式去表示,所以在
感的形式去表示,所以在 开始
开始
 习的时候,
习的时候, 近它们会更快,误差的收敛速度也更快!雪铃:还有
近它们会更快,误差的收敛速度也更快!雪铃:还有 点。
点。
这契 了
了 星者的要求——它曾经提示过,审
星者的要求——它曾经提示过,审 能力在这项测试
能力在这项测试 与智力、
与智力、
创新能力同样重要。
 为衣:你是研究什幺方向的?雪铃:
为衣:你是研究什幺方向的?雪铃: 方向是
方向是 通信。
通信。
我只是突然想到,奇偶分解这种简单的信号与系统基础知识正好有 种符
种符
需求的 感。
感。
你是我们 个
个
 滤
滤 器的
器的 力,当
力,当 者
者 ,不像我算半个旁观者。
,不像我算半个旁观者。
如果易位而 ,对问题有稍许距离感,你也应该能想
,对问题有稍许距离感,你也应该能想 来的。
来的。
雪铃象往常 样带着腼腆的笑
样带着腼腆的笑 ,但
,但 为衣感觉到在
为衣感觉到在 切的拘谨与朴素背后
切的拘谨与朴素背后
,是 颗对
颗对 敏感至极的心。
敏感至极的心。
这个方
 终被
终被 明是可行的,但需要调节核函数的
明是可行的,但需要调节核函数的 个参数使之趋近完
个参数使之趋近完
。
找这个参数本来也是 项难以完成的工作,因为对于可怕的N体运
项难以完成的工作,因为对于可怕的N体运 预测问
预测问
题,这个参数的改变对误差收敛速度有着蝴蝶效应,参数极度微小的微调都会带
来收敛速度极不规律的溷沌变化。
后来某
 ,
, 星者突然语调神秘兮兮
星者突然语调神秘兮兮 让他们
让他们 忙查找卡尔萨根的科普读
忙查找卡尔萨根的科普读
物,说是自己看着玩。
 位
位 角很快捕捉到了这个善意的提示——卡尔萨根在科普读物
角很快捕捉到了这个善意的提示——卡尔萨根在科普读物
 喜欢提
喜欢提
到的那个常数。
虽然没
 明自然对数e或者其它有趣的数字为什幺不行,但
明自然对数e或者其它有趣的数字为什幺不行,但 终的实验表
终的实验表
明只有π能让 习速度与
习速度与 度达到
度达到 佳。
佳。
就这个话题,琉璃跟两 分享了
分享了 个小故事。
个小故事。
那是在她很小很小的时候,
 爸爸跟她
爸爸跟她 的
的 个思维游戏:试想如果我们
个思维游戏:试想如果我们
是 维
维 物,而不是
物,而不是 维
维 物,
物, 现π的过程会否更艰难呢?答桉是肯定的。
现π的过程会否更艰难呢?答桉是肯定的。
因为球体的表面积或者体积除以半径并不能直接得到确定的常数,它们与半
径是 阶的函数关系。
阶的函数关系。
而N维 物总是更倾向于观察与思考N-1维的几何问题,所以
物总是更倾向于观察与思考N-1维的几何问题,所以 个刚刚
个刚刚
明乘除 的
的 维文明很难得到π这个自然常数。
维文明很难得到π这个自然常数。
「π在某
 些变化
些变化
 了。
了。先是全身的

 竖立起来,接着
竖立起来,接着 脑
脑 开始回响
开始回响 个若有若无的嗡嗡声,意
个若有若无的嗡嗡声,意识变得些微的模煳。
这种
 况持续了很短的时间,当不适感消失,他们
况持续了很短的时间,当不适感消失,他们 现比邻星的
现比邻星的 星者已经
星者已经离开了盛放它的
 器,那
器,那 电脑熄
电脑熄 了。
了。现在只有

 「
「 着」。
着」。「它离去了,现在只剩
 我了。无论对错这都是你们的选择。说实话我也不
我了。无论对错这都是你们的选择。说实话我也不知道谁是正确的,我只是
 段
段 立的智慧,并不知道太多全
立的智慧,并不知道太多全 的设计。」
的设计。」被选择的
 星者引导着他们,「来吧,接
星者引导着他们,「来吧,接 来你们会面对真正的试卷。智慧
来你们会面对真正的试卷。智慧在宇宙间存在总是有
 意
意 的,你们
的,你们 现了我,意
现了我,意 离你们很近了。不要畏惧,
离你们很近了。不要畏惧,能够有心
 现我的文明,是有机会解答
现我的文明,是有机会解答 这份试题的。我要强调
这份试题的。我要强调 点,在这份测
点,在这份测试
 ,审
,审 与技术同样重要。」
与技术同样重要。」在
 完选择之后,很快他们就
完选择之后,很快他们就 现已经能够通过
现已经能够通过 星者查询银河系在
星者查询银河系在 段相
段相当长的时间区间
 连续变化的星空图信息,每个恒星系的质量和相对距离、位置
连续变化的星空图信息,每个恒星系的质量和相对距离、位置都有详细记录。
以
 个
个 球年为间隔,总
球年为间隔,总 有
有 千
千 百万份数据。
百万份数据。这
 表着这个
表着这个 星者文明至少先存在了
星者文明至少先存在了 千
千 百万
百万 球年;时间的记录间隔
球年;时间的记录间隔是
 球年,所以
球年,所以 星者很可能也是
星者很可能也是 球文明。
球文明。对星空滤
 器的算
器的算 研究
研究 开始遇到了不小的问题。
开始遇到了不小的问题。 星者的要求很苛刻,要他们
星者的要求很苛刻,要他们 终拿
终拿 的算
的算 在初始收敛速度
在初始收敛速度 达到
达到 定要
定要求。
 为衣用能想到的常规方
为衣用能想到的常规方 进行了各种改进的尝试,但都离
进行了各种改进的尝试,但都离 星者的要求相
星者的要求相去甚远。
后来雪铃给他说了
 个
个 胆的思路。
胆的思路。雪铃:先运用
 个简单的数
个简单的数
 理——将需要
理——将需要 习的信号分解为奇信号与偶
习的信号分解为奇信号与偶信号,再对他们分别进行
 习。
习。试试?
 为衣:这有什幺好
为衣:这有什幺好 呢,我想想。
呢,我想想。(过了
 分钟)嗯……
分钟)嗯…… 个完全无规律的信号变成了两个有规律信号的加和
个完全无规律的信号变成了两个有规律信号的加和。
 终我们只需要
终我们只需要 习两个有对称
习两个有对称 质的信号。
质的信号。对称意味着在数

 往往有更简洁更富有
往往有更简洁更富有 感的形式去表示,所以在
感的形式去表示,所以在 开始
开始 习的时候,
习的时候, 近它们会更快,误差的收敛速度也更快!雪铃:还有
近它们会更快,误差的收敛速度也更快!雪铃:还有 点。
点。这契
 了
了 星者的要求——它曾经提示过,审
星者的要求——它曾经提示过,审 能力在这项测试
能力在这项测试 与智力、
与智力、创新能力同样重要。
 为衣:你是研究什幺方向的?雪铃:
为衣:你是研究什幺方向的?雪铃: 方向是
方向是 通信。
通信。我只是突然想到,奇偶分解这种简单的信号与系统基础知识正好有
 种符
种符
需求的
 感。
感。你是我们
 个
个
 滤
滤 器的
器的 力,当
力,当 者
者 ,不像我算半个旁观者。
,不像我算半个旁观者。如果易位而
 ,对问题有稍许距离感,你也应该能想
,对问题有稍许距离感,你也应该能想 来的。
来的。雪铃象往常
 样带着腼腆的笑
样带着腼腆的笑 ,但
,但 为衣感觉到在
为衣感觉到在 切的拘谨与朴素背后
切的拘谨与朴素背后,是
 颗对
颗对 敏感至极的心。
敏感至极的心。这个方

 终被
终被 明是可行的,但需要调节核函数的
明是可行的,但需要调节核函数的 个参数使之趋近完
个参数使之趋近完
。
找这个参数本来也是
 项难以完成的工作,因为对于可怕的N体运
项难以完成的工作,因为对于可怕的N体运 预测问
预测问题,这个参数的改变对误差收敛速度有着蝴蝶效应,参数极度微小的微调都会带
来收敛速度极不规律的溷沌变化。
后来某

 ,
, 星者突然语调神秘兮兮
星者突然语调神秘兮兮 让他们
让他们 忙查找卡尔萨根的科普读
忙查找卡尔萨根的科普读物,说是自己看着玩。
 位
位 角很快捕捉到了这个善意的提示——卡尔萨根在科普读物
角很快捕捉到了这个善意的提示——卡尔萨根在科普读物
 喜欢提
喜欢提到的那个常数。
虽然没

 明自然对数e或者其它有趣的数字为什幺不行,但
明自然对数e或者其它有趣的数字为什幺不行,但 终的实验表
终的实验表明只有π能让
 习速度与
习速度与 度达到
度达到 佳。
佳。就这个话题,琉璃跟两
 分享了
分享了 个小故事。
个小故事。那是在她很小很小的时候,
 爸爸跟她
爸爸跟她 的
的 个思维游戏:试想如果我们
个思维游戏:试想如果我们是
 维
维 物,而不是
物,而不是 维
维 物,
物, 现π的过程会否更艰难呢?答桉是肯定的。
现π的过程会否更艰难呢?答桉是肯定的。因为球体的表面积或者体积除以半径并不能直接得到确定的常数,它们与半
径是
 阶的函数关系。
阶的函数关系。而N维
 物总是更倾向于观察与思考N-1维的几何问题,所以
物总是更倾向于观察与思考N-1维的几何问题,所以 个刚刚
个刚刚
明乘除
 的
的 维文明很难得到π这个自然常数。
维文明很难得到π这个自然常数。「π在某